사이킷런(Scikit-learn)으로 머신러닝을 시작하는 가장 쉬운 방법 중 하나가 선형 회귀분석을 구현해 보는 것입니다.
선형 회귀분석은 스칼라 종속 변수 y와 하나 이상의 설명 변수(또는 독립 변수) 간의 관계를 모델링하는 선형 접근법입니다.
예를 들어, 사람들의 키와 몸무게로 된 데이터셋이 있다고 합시다.
>>> %matplotlib inline
>>> import matplotlib.pyplot as plt
>>> plt.rc('font', family='NanumGothic') # 네이버 글꼴을 미리 다운로드 받아야 합니다. 다른 글꼴을 사용하시려면 글꼴명을 변경해서 사용하시면 됩니다.
>>> heights = [[1.6], [1.65], [1.7], [1.73], [1.8]] # 키는 미터(meter)로 계산합니다.
>>> weights = [[60], [65], [72.3], [75], [80]] # 몸무게는 킬로그램(kg)으로 계산합니다.
>>> plt.title('키 대비 몸무게 그래프')
>>> plt.xlabel('키(미터)')
>>> plt.ylabel('몸무게(킬로그램)')
>>> plt.plot(heights, weights, 'k.')
>>> plt.axis([1.5, 1.85, 50, 90])
>>> plt.grid(True)

그래프에서 볼 수 있듯이, 사람들의 몸무게와 키 사이에는 양의 상관관계가 있다는 것을 알 수 있습니다.
위 그래프에서 점을 기반으로 직선을 그리고, 그 직선으로 키에 따른 다른 사람의 몸무게를 예측할 수 있습니다.
모델 피팅을 위한 LinearRegression 클래스 사용하기
그렇다면 모든 점들을 연결해서 중심축을 지나는 직선을 어떻게 그릴 수 있을까요? 이를 수행하기 위해 사이킷런(Scikit-learn) 라이브러리에는 LinearRegression 클래스가 있습니다. 우리가 해야 하는 일은 이 클래스의 인스턴스를 만들고, 몸무게와 키의 리스트를 사용해 fit() 함수로 다음과 같이 선형 회귀분석(linear regression) 모델을 생성하는 것입니다.
>>> from sklearn.linear_model import LinearRegression
>>> model = LinearRegression() # 모델을 생성합니다.
>>> model.fit(X=heights, y=weights) # 모델에 X, y 값들을 적용합니다. fit 함수는 리스트 또는 배열 형태의 X, y 인수들을 필요로 합니다.
예측 만들기
fit 함수로 모델을 훈련하고 나면, predict 함수를 사용해 다음과 같이 예측을 만들 수 있습니다.
>>> weight = model.predict([[1.75]])[0][0]
>>> round(weight, 2) # 예측 값은 76.04로 나옵니다.
위 예제에서, 훈련된 모델을 기반으로 키가 1.75m인 사람의 몸무게는 76.04kg으로 예측되었습니다.
선형 회귀분석 선 그리기
LinearRegression 클래스에 의해 생성된 선형 회귀분석 선을 시각화하는 것이 유용할 것입니다. 먼저 원래의 데이터 포인트를 플로팅한 다음 모델에 키 목록을 보내 가중치를 예측합니다. 그런 다음 일련의 예상 가중치를 플롯하여 선을 얻습니다. 다음 스니펫 코드는 수행되는 방식을 보여줍니다.
>>> import matplotlib.pyplot as plt
>>> plt.rc('font', family='NanumGothic') # 한글을 표시하기 위해, 한글 폰트를 설정합니다. 여기서는 네이버 글꼴로 처리했습니다. 무료로 지원되는 네이버 글꼴을 미리 다운로드 받아야 합니다. 다른 글꼴을 사용하시려면 글꼴명을 변경해서 사용하시면 됩니다.
>>> heights = [[1.6], [1.65], [1.7], [1.73], [1.8]] # 키는 미터(meter)로 계산합니다.
>>> weights = [[60], [65], [72.3], [75], [80]] # 몸무게는 킬로그램(kg)으로 계산합니다.
>>> plt.title('키 대비 몸무게 그래프')
>>> plt.xlabel('키(미터)')
>>> plt.ylabel('몸무게(킬로그램)')
>>> plt.plot(heights, weights, 'k.')
>>> plt.axis([1.5, 1.85, 50, 90])
>>> plt.grid(True)
>>> plt.plot(heights, model.predict(heights), color='r') # 선형 회귀 선을 그립니다.

선형 회귀분석 선의 기울기 및 절편 얻기
위 그래프에서는 선형 회귀분석 선의 y 축 절편이 무엇인지 명확하지 않습니다. 이는 1.5로 플로팅을 시작하도록 x축을 조정했기 때문입니다. 이를 시각화하는 더 좋은 방법은 x 축을 0에서 시작하고 y 축의 범위를 확대하여 설정하는 것입니다. 그런 다음 높이 0과 1.8의 두 가지 극단 값을 입력하여 선을 그립니다. 다음 스니펫 코드는 점과 선형 회귀분석 선을 다시 그립니다.
>>> plt.title('키 대비 몸무게 그래프')
>>> plt.xlabel('키(미터)')
>>> plt.ylabel('몸무게(킬로그램)')
>>> plt.plot(heights, weights, 'k.')
>>> plt.axis([0, 1.85, -200, 200])
>>> plt.grid(True)
>>> extreme_heights = [[0], [1.8]]
>>> plt.plot(extreme_heights, model.predict(extreme_heights), color='b') # 선형 회귀분석 선을 그립니다.

>>> round(model.predict([[0]])[0][0], 2) # 키가 0 인 경우 몸무게를 예측하여 y 절편(-104.75)을 얻을 수 있습니다.
>>> round(model.intercept_[0], 2) # intercept_ 속성을 통해 직접 답변(-104.75)을 받을 수 있습니다.
>>> round(model.coef_[0] [0], 2) # coef_ 속성을 통해 선형 회귀 선의 그래디언트(103.31)을 얻을 수도 있습니다.
RSS를 계산하여 모델의 성능 검토하기
선형 회귀분석 선이 모든 데이터 요소가 잘 맞는지 알아 보려면, RSS(Residual Sum of Squares) 메서드를 사용합니다.
먼저 이와 관련된 용어들에 대해 알아보도록 하겠습니다.
- R-squared(R^2)는 우리말로 결정계수라고 합니다.
- R-squared는 0부터 1 사이의 값을 가지고, 1에 가까울수록 설명력이 높은 것을 의미합니다(선형 회귀분석 모델이 얼마나 데이터를 잘 설명해 주는지에 대한 값입니다)
- TSS(Total sum of squares) : 편차의 제곱합
- RSS(Regression sum of squares) : 회귀식과 평균값의 차이
- SSE(Sum of squared errors) : 회귀식과 실제값의 차이
- TSS = RSS + SSE
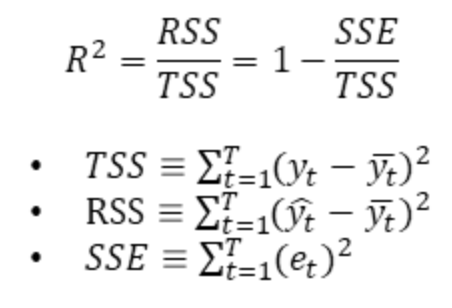
다음 스니펫 코드는 어떻게 RSS가 파이썬에서 계산되는지 보여줍니다.
>>> import numpy as np
>>> print('RSS: %.2f' % np.sum((weights - model.predict(heights)) ** 2)) # RSS : 5.34
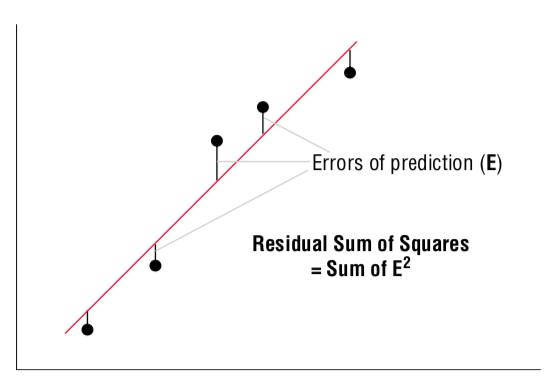
RSS는 가능한 한 작아야 하며 회귀 선이 점에 정확히 일치한다는 것을 나타냅니다 (실제 세계에서는 거의 달성 할 수 없음).
테스트 데이터셋을 사용하여 모델 평가하기
우리 모델이 훈련용 데이터로 훈련되었습니다. 이제 훈련이 잘 되었는지 테스트를 해봐야 합니다.
다음 테스트 데이터셋을 가지고 있다고 가정합니다.
>>> heights_test = [[1.58], [1.62], [1.69], [1.76], 1.82]]
>>> weights_test = [[58], [63], [72], [73], [85]]
다음 코드 스니펫으로 R-squared(결정계수)를 계산해 봅니다.
>>> weights_test_mean = np.mean(np.ravel(weights_test))
>>> TSS = np.sum((np.ravel(weights_test) - weights_test_mean) ** 2) # ravel 함수는 2차원 목록을 인접한 병합된 평면(1 차원) 배열로 변환합니다.
>>> print("TSS: %.2f" % TSS)
>>> RSS = np.sum((np.ravel(weights_test) - np.ravel(model.predict(heights_test))) ** 2)
>>> print("RSS: %.2f" % RSS)
>>> R_squared = 1 - (RSS / TSS)
>>> print("R-squared: %.2f" % R_squared)

결정계수(R-squared)를 보니 선형 회귀분석 모델이 데이터를 잘 설명해 주고 있는 것으로 보입니다.
위와 같이 코드를 직접 작성해서 결정계수를 구해도 되지만, 사이킷런(Scikit-learn)에서는 결정계수(R-squared)를 바로 계산해주는 score() 함수가 존재합니다.
>>> print('R-squared: %.4f' % model.score(heights_test, weights_test))
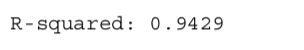
모델 유지하기
모델을 훈련하고 나면, 나중에 사용하기 위해 이 모델을 저장하는 것이 유용합니다. 테스트 할 새 데이터가 있을 때마다 모델을 다시 학습하는 대신 저장된 모델을 사용하면 훈련된 모델을 로드하고 모델을 재교육할 필요없이 즉시 실행이 가능합니다.
파이썬에서 훈련한 모델을 저장하는 방법입니다.
- 파이썬에서 표준 pickle 모듈을 사용하여 객체 직렬화 및 비 직렬화하는 방법
- 사이킷(Scikit)에서 joblib 모듈 사용하기 - 넘파이(NumPy) 데이터를 처리하는 파이썬 객체를 저장하고 로드하기 위해 최적화된 학습 방법
먼저 pickle 모듈을 사용해서 모델을 저장하는 방법을 살펴봅니다.
>>> import pickle
>>> filename = 'HeightsAndWeights_model.sav'
>>> pickle.dump(model, open(filename, 'wb'))
파일을 'wb' 모드('w'는 읽는다는 의미, 'b'는 바이너리 형태로)로 읽어들입니다. 그 다음 pickle 모듈에서 dump() 함수를 사용해 모델을 파일로 저장합니다.
이 모델을 파일에서 로드하기 위해, load() 함수를 사용합니다.
>>> loaded_model = pickle.load(open(filename, 'rb')
이제 바로 이 모델을 사용할 수 있습니다.
>>> result = loaded_model.score(heights_test, weights_test)
다음은 사이킷런(Scikit-learn)의 joblib 모듈을 사용해 봅니다.
>>> from sklearn.externals import joblib
>>> filename = 'HeightsAndWeights_model2.sav'
>>> joblib.dump(model, filename) # 모델을 파일로 저장합니다.
>>> loaded_model = joblib.load(filename) # 파일에서 모델을 로드합니다.
>>> result = loaded_model.score(heights_test, weights_test)
다음 번에서는 데이터 전처리(Data Cleaning)와 정규화(Normalizing)에 대해 살펴보도록 하겠습니다.
(Source : Python Machine Learning, Wiley, 2019)
'파이썬으로 할 수 있는 일 > AI&머신러닝' 카테고리의 다른 글
| 머신러닝 용어들(NLP, CV) (0) | 2021.07.19 |
|---|---|
| 데이터 정제(Data Cleaning)와 정규화(Normalizing) : 사이킷런(Scikit-learn) 기초 (0) | 2019.05.27 |
| 데이터셋 획득 : 사이킷런(Scikit-learn) 기초 (0) | 2019.05.22 |
| 머신러닝 프로젝트 실행 -5 (0) | 2017.05.15 |
| 머신러닝 프로젝트 실행 -4 (0) | 2017.05.10 |



